Exponentielles Wachstum

In letzter Zeit war oft die Rede von exponentiellem Wachstum. Ein Begriff, der vielen Leuten, insbesondere Nicht-Mathematikern, wenig bis gar nicht vertraut ist. 

Nun, Dinge können, vereinfacht gesagt, linear wachsen oder nicht linear. 

Lineares Wachstum ist leicht erklärt. Stellen Sie sich vor, Sie kaufen einen Sack Reis zum Preis von 10 EUR. Wenn Sie zwei  Säcke haben wollen, müssen Sie das Doppelte, also 20 EUR berappen. Bei drei Säcken das Dreifache und so weiter. Graphisch sieht das dann so aus:

Bild 1: Lineare Funktion

Nicht-lineares Wachstum (in diesem Fall: exponentielles) ist anders. Stellen Sie sich vor, ein neuartiges Virus entweicht versehentlich aus einem Forschungslabor. Rein hypothetisch natürlich. 

Am Anfang (Woche 0) trägt nur ein Mensch das ansteckende Virus in sich. Ab dann verdoppelt sich die Zahl der Träger in jeder Woche. Wir haben dann in Woche 1 zwei Neuinfizierte, in Woche 2 vier und in Woche 3 acht. 

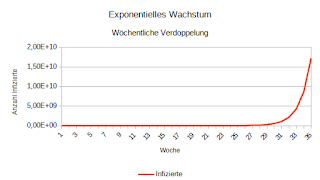
Bis zur 27. Woche sieht der Graph dann so aus: 

Bild 2: Exponentialfunktion mit wöchentlicher Verdoppelung

Man beachte die Einheiten auf der senkrechten (y) Achse. Anfangs sieht es so aus, als wäre die Kurve immer nahe der Nulllinie. Dem ist aber nicht so, der Maßstab verzerrt hier den Eindruck. 

Sehen wir uns einige markante Punkte an, um ein Gefühl für die Zahlen zu bekommen. In der 20. Woche infizieren sich 524 288 Menschen mit dem Virus. Das entspricht ungefähr der Bevölkerung Luxemburgs. 

In der 24. Woche zählt man dann fast 8,4 Millionen Neuinfizierte, also in etwa die Bevölkerung Österreichs. 

Und wenig später, in der 27. Woche gibt es fast 70 Millionen neue Fälle, das kommt der Bevölkerungszahl Deutschlands schon recht nahe.  

Lassen wir die Funktion weiterlaufen bis zur 35. Woche. Wie sieht das dann aus? 

Hier ist die Graphik:

Bild 3: Exponentialfunktion mit wöchentlicher Verdoppelung

Die Bilder 2 und 3 sehen einander sehr ähnlich. Der wesentliche Unterschied ist in der senkrechten Achse zu finden. Denn während Bild 2 in der 27. Woche bei mehr als 67 Millionen aufhört, endet Bild 3 in der 35. Woche bei mehr als 17 Milliarden, in etwa dem Doppelten der gegenwärtigen Weltbevölkerung. 

Mit anderen Worten: Bei einem rein exponentiellen Anstieg der Infektionen ist nach etwas mehr als einem halben Jahr die gesamte Weltbevölkerung infiziert. Soweit die Mathematik. 

Die Realität sieht anders aus. Nehmen wir die drei genannten Länder und sehen wir uns die tatsächlichen (kumulierten) "Fallzahlen" an. Stichtag: 16. April 2021. Daten aus Worldometer. 

Luxemburg:    64 549 

Österreich:      589 299

Deutschland:   3 095 016

Welt:                139 816 716

Wir sind jetzt schon deutlich länger als ein Jahr mit einem Virus konfrontiert, das sich über den ganzen Globus ausgebreitet hat. Und nach obigem Modell müsste inzwischen jeder Erdenbürger mit dem Virus Bekanntschaft gemacht haben. Das ist aber offensichtlich nicht so, wie die Zahlen klar zeigen. 

Wie kann man sich diesen Widerspruch erklären? 

Die Welt ist eben kein Mathematiklabor. Zwar gibt es durchaus kurze Phasen, in denen ein exponentieller Verlauf zu erkennen ist. Allerdings ist das nie länger als ein paar kurze Wochen. Spätestens dann ist die Exponentialfunktion sozusagen zu Ende und ein anderer Verlauf tritt an ihre Stelle. 

Ohne ins Detail zu gehen, hier einige mögliche Gründe dafür. 

Im Allgemeinen sind einmal Infizierte ja nicht ständig krank, sondern werden (nach einigen Wochen) wieder gesund oder sie sterben. Dadurch verringert sich der Pool der Infizierten und gleichzeitig erhöht sich die Anzahl der (zumindest zeitweilig) Immunisierten. 

Wenn sich eine Krankheit epidemisch ausbreitet, reagiert die Bevölkerung auf die Gefahr und passt ihr Verhalten an. Dadurch verringert sich die Übertragungsgeschwindigkeit des Virus. Bessere Hygiene, Abstand und die Vermeidung größerer Menschenansammlungen reduzieren die Ausbreitung des Erregers.